Update 14 April 2024: I’ve discovered that it is not necessary to calculate bitmask values for the ext1 external wakeup with the ESP32. There are predefined definitions that you can use. If you are interested check out my post ESP32: Wakeup from multiple GPIO sources and using predefined pin definitions instead of bitmask
I’m currently learning how to use the deep sleep functionality for ESP32. I’ve been following the excellent article by Random Nerd Tutorials ESP32 Deep Sleep with Arduino IDE and Wake Up Sources. I recommend this article if like me you are starting out with deep sleep with the ESP32.
I want my ESP32 to wake up from any one of three external inputs and External Wake Up (ext1) looks like the best option for this. Rather than directly specifying pins, there is a more elaborate method that requires calculating a bitmask that is a combination of all pins. The bitmask value is then used in this command:
esp_sleep_enable_ext1_wakeup(bitmask, mode)The bitmask value is calculated using this:
- Calculate 2^(GPIO_NUMBER) for each of the pins.
- Add the totals together.
- Convert to hex. Can use rapidtables.com/convert/number/decimal-to-hex.html to do this.
- Use the hex number you’ve obtained in the bitmask variable.
I am using three pins; 27, 32 and 33. For these I need to start by calculating this: 2^27 + 2^32 + 2^33. I started by getting out my ancient trusty Casio calculator and entered 2^27. The result 1.34217 08. Hmmm looks like scientific notation if I remember back 40 years correctly. Doesn’t look promising as it doesn’t have enough digits.
I thought I would try a few things to see what is the easiest way I could calculate it.
Just to see what we have to end up with this is this is the full calculation:
= 2^27 + 2^32 + 2^33 = 134217728 + 4294967296 + 8589934592 = 13019119616 Hex = 0x308000000
I started by entering 2^27 directly into Google search. Nice, it gave the result 134217728
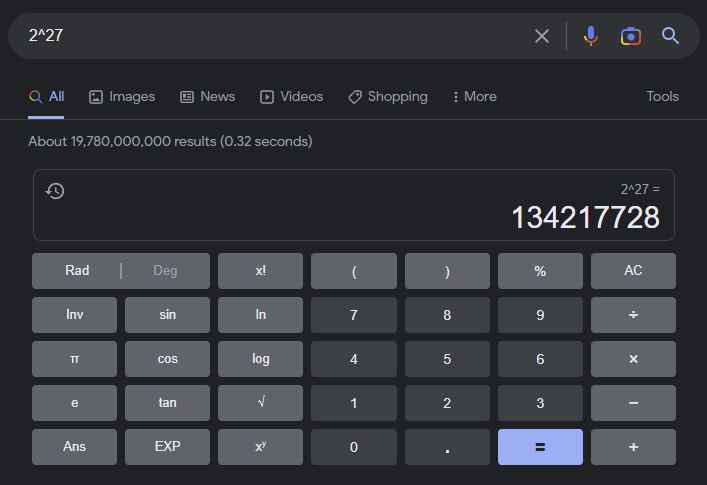
Next I tried entering 2^27 + 2^32 + 2^33 into Google search. Result: 13019119616. Impressive.
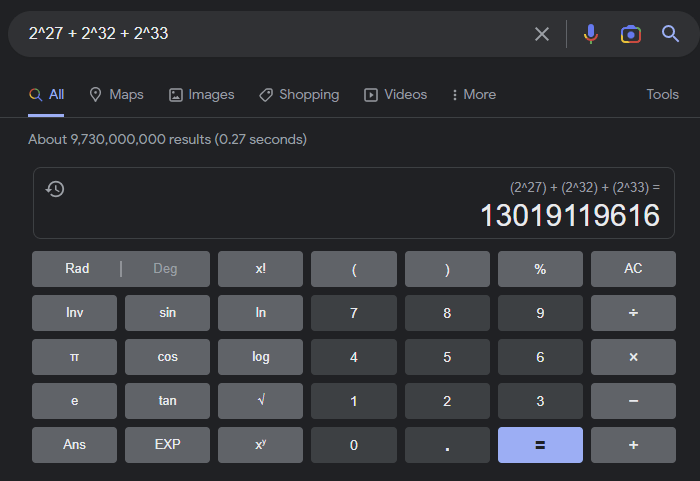
Finally I entered convert 2^27 + 2^32 + 2^33 to hex into the Google search. Result: 0x308000000
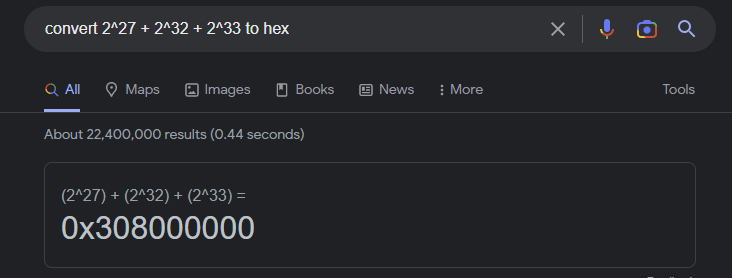
Very cool and simpler than I was expecting. I’m happy that I know how to manually do the calculation and also that I have an easy way to do it.
I mentioned this in the other post, but just to put your engagement scores to the moon tonight…You can also have the compiler do this. You just have to know slightly funny spellings because you’re shifting more than 32 bits on a 32-bit CPU. Therefore, you’re not working with ‘integers’, you’re using ‘long long’. We could use uint64_t, but that actually makes more work for ourselves.The spelling is 1ULL << 27 | 1ULL << 32 | 1ULL << 33Read aloud to the class, that’s “one unsigned long long, shifted left 27 bits logically ored with one unsigned long …[ repeats]”.We can even show you what the compiler does. Pop open:https://godbolt.org/z/4nExKvssbThe obvious function returns a constant that comes from the above. Well, the above came from that function, but you don’t need to know the order of which I typed and which I copied. 🙂 main() just prints it.Now if you look in the middle, we load the return value (register AX) with a number. Does that number look familar? Yes, yes it does.Now over on the right is what it would have printed. This web thingy can generate XTensa code, but can’t run it. Aside from the textual substitution, this is exactly what’s happening when you started using names anyway. This is one of the few cases where using the number might actually be easier, but there are cases where there’s not a 1:1 mapping of bits and values inside CPU registers like this.Still, even if you don’t adopt using this style as your daily driver, learning about goldbolt is a trick that all your readers should know about. YES, it can do xtensa and C++ and so on. It’s SUPER handy to figure out if something was legal in GCC 10.0 but not 9.1 or whatever; it’s just a few twists of the knobs to run most any compiler that matters in a way that’s super easy to study the generated code.Enjoy!
LikeLike
I’m starting to understand this a bit better but confess I have some way to go. The number in Gobolt does look familiar. I had not come across that tool. It’s interesting. I’ll have to investigate it further, but my understanding of coding is really fairly basic at this stge. I hope others find it useful. I think you have pushed my engagement scores up. The days viewing stats nearly doubled 🙂
LikeLike